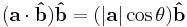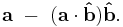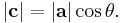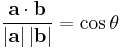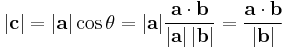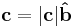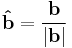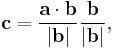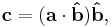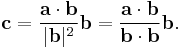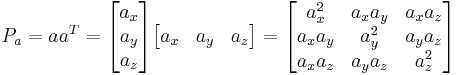Vector projection

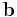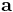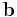The vector projection (also known as the vector resolute, or vector component) of a vector $\mathbf{a}$ in the direction of a vector $\mathbf{b}$ (or "of $\mathbf{a}$ on/onto $\mathbf{b}$ "), is given by:

$(\mathbf{a}\cdot\mathbf{\hat b})\mathbf{\hat b} = (|\mathbf{a}|\cos\theta)\mathbf{\hat b}$

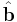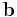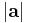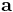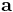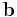where the operator $\cdot$ denotes a dot product, $\hat{\mathbf{b}}$ is the unit vector in the direction of $\mathbf{b}$ , $|\mathbf{a}|$ is the length of $\mathbf{a}$ , and $\theta$ is the angle between $\mathbf{a}$ and $\mathbf{b}$ .

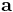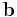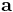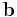The other component of $\mathbf{a}$ (perpendicular to $\mathbf{b}$ ), called the vector rejection of $\mathbf{a}$ from $\mathbf{b}$ , is given by:

$\mathbf{a}\ -\ (\mathbf{a}\cdot\mathbf{\hat b})\mathbf{\hat b}.$

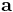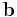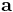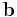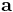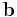Both the vector projection and the vector rejection are vectors. The vector projection of $\mathbf{a}$ on $\mathbf{b}$ is the orthogonal projection of $\mathbf{a}$ onto the straight line defined by $\mathbf{b}$ . The corresponding vector rejection is the orthogonal projection of $\mathbf{a}$ onto a plane orthogonal to $\mathbf{b}$ .

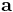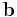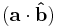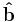The vector projection of $\mathbf{a}$ on $\mathbf{b}$ can be also regarded as the corresponding scalar projection $(\mathbf{a}\cdot\mathbf{\hat b})$ multiplied by $\mathbf{\hat b}$ .

1 Overview
2 Matrix representation
3 Uses
4 References
5 See also

Overview

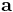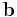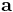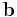If $\mathbf{a}$ and $\mathbf{b}$ are two vectors, the projection of $\mathbf{a}$ on $\mathbf{b}$ is the vector 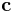$\mathbf{c}$ with the same direction as 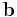$\mathbf{b}$ and with the length:

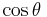$|\mathbf{c}| = |\mathbf{a}| \cos \theta .$

When $\theta$ is not known, we can compute $\cos \theta \,$ using the following property of the dot product $\mathbf{a} \cdot \mathbf{b}$ :

$\frac {\mathbf{a} \cdot \mathbf{b}} {|\mathbf{a}| \, |\mathbf{b}|} = \cos \theta \,$

Thus, the length of 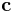$\mathbf{c}$ can be also computed as follows:

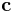$|\mathbf{c}| = |\mathbf{a}| \cos \theta = |\mathbf{a}| \frac {\mathbf{a} \cdot \mathbf{b}} {|\mathbf{a}| \, |\mathbf{b}|} = \frac {\mathbf{a} \cdot \mathbf{b}} {|\mathbf{b}| }\,$

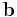Since $\mathbf{c}$ is in the same direction as $\mathbf{b}$ ,

$\mathbf{c} = |\mathbf{c}| \mathbf{\hat b}$

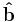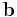where $\mathbf{\hat b}$ is the unit vector with the same direction as $\mathbf{b}$ :

$\mathbf{\hat b} = \frac {\mathbf{b}} {|\mathbf{b}|}\,$

Substituting for |c| defines c in terms of a and b

$\mathbf{c} = \frac {\mathbf{a} \cdot \mathbf{b}} {|\mathbf{b}| } \frac {\mathbf{b}} {|\mathbf{b}|},$

which is equivalent to either

$\mathbf{c} = (\mathbf{a} \cdot \mathbf{\hat b}) \mathbf{\hat b},$

or^[1]

$\mathbf{c} = \frac {\mathbf{a} \cdot \mathbf{b}} {|\mathbf{b}|^2}{\mathbf{b}} = \frac {\mathbf{a} \cdot \mathbf{b}} {\mathbf{b} \cdot \mathbf{b}}{\mathbf{b}}.$

The latter formula is computationally more efficient than the former. Both require two dot products and eventually the multiplication of a scalar by a vector, but the former additionally requires a square root and the division of a vector by a scalar,^[2] while the latter additionally requires only the division of a scalar by a scalar.

Matrix representation

The orthogonal projection can be represented by a projection matrix. To project a vector onto the unit vector a = (a_x, a_y, a_z), it would need to be multiplied with this projection matrix:

$P_a = a a^T = \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix} \begin{bmatrix} a_x & a_y & a_z \end{bmatrix} = \begin{bmatrix} a_x^2 & a_x a_y & a_x a_z \\ a_x a_y & a_y^2 & a_y a_z \\ a_x a_z & a_y a_z & a_z^2 \\ \end{bmatrix}$

Uses

The vector projection is an important operation in the Gram-Schmidt orthonormalization of vector space bases. It is also used in the Separating axis theorem to detect if two convex shapes intersect.

References

^ "Dot Products and Projections". http://www.math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/vcalc/dotprod/dotprod.html.
^ The second dot product, the square root and the division are not shown, but they are needed to compute 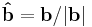$\mathbf{\hat b} = {\mathbf{b}} / {|\mathbf{b}|}$ (for more details, see the definition of Euclidean norm).

Vector projection

Contents

Overview

Matrix representation

Uses

References

See also